The importance of turbulence in the ocean

The ocean maintains steady state stratification. Without turbulent mixing, the ocean would not be stratified. But how is this stratification maintained?

The downwelling vertical transport in regions of deep water formation (North Atlantic, Antarctic shelves) must be balanced by upwelling vertical transport (part from upwelling at the Antarctic Polar Front of the Antarctic Circumpolar Current, and the rest a small upwelling distributed through the ocean). This small upwelling, \(w\), is a key component contributing the steady state ocean and related to the eddy diffusivity.

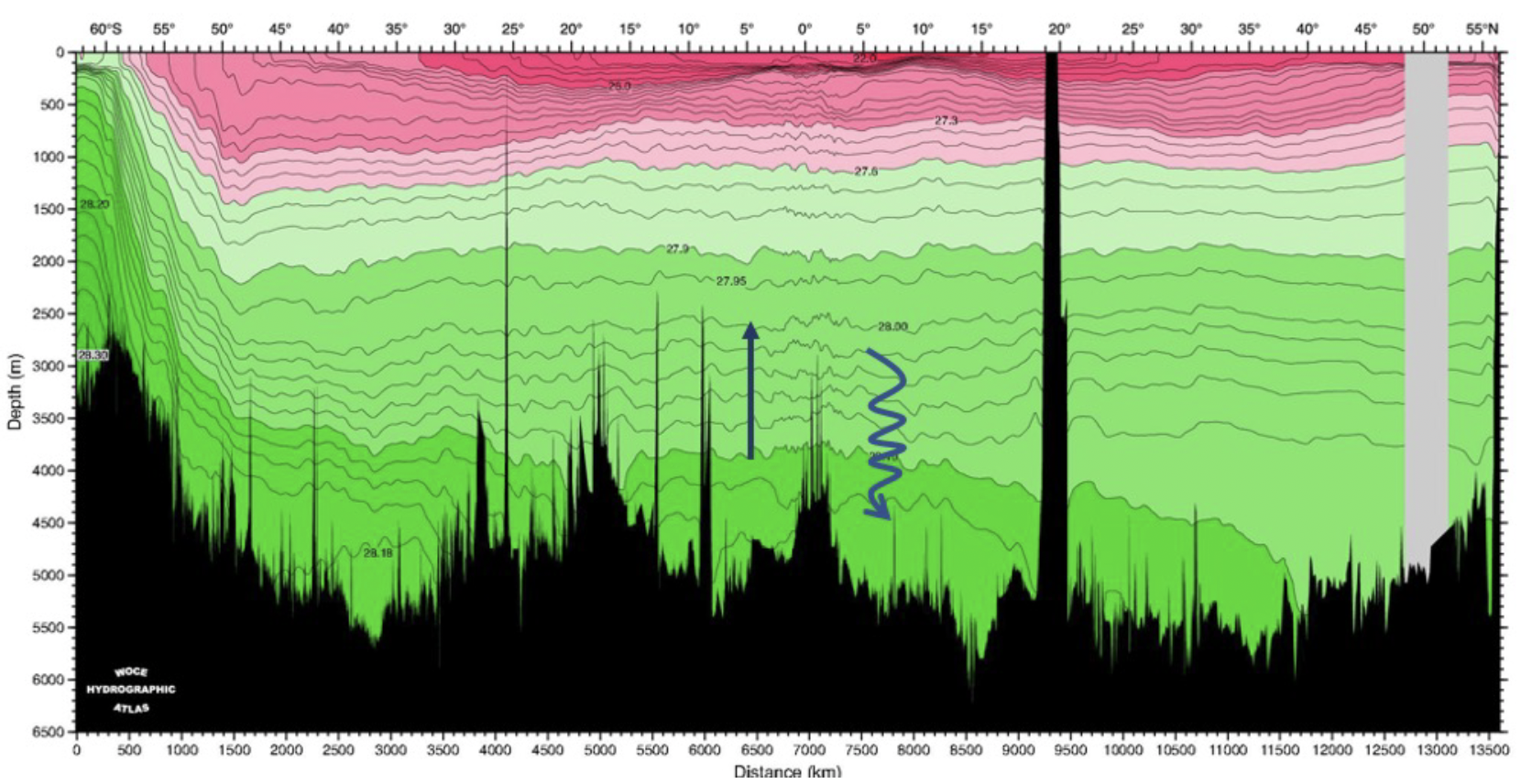
Fig. 20 WOCE, Section P16, Neutral Density

Taking the continuity equation for 1D flow in a steady ocean:

\[ \cancel{u \frac{\partial b}{\partial x}} + \cancel{v \frac{\partial b}{\partial y}} + w \frac{\partial b}{\partial z} \approx \frac{\partial }{\partial z}(K_z \frac{\partial b}{\partial z}), \]

some diffusion of heat is required to balance the vertical transport of water upwards.

Walter Munk [Mun95] took a vertical profile of temperature to 4000 m and, by fitting an exponential curve \(f(z,K_z,w)\) to an observed buoyancy profile, deduced the eddy diffusivity, \(K_z\), required to maintain the observed stratification ~ 10\(^{-4}\) m\(^2\)s\(^{-1}\). This number has since been observed in parts of the ocean, but found to be heterogeneous [PTLS97].

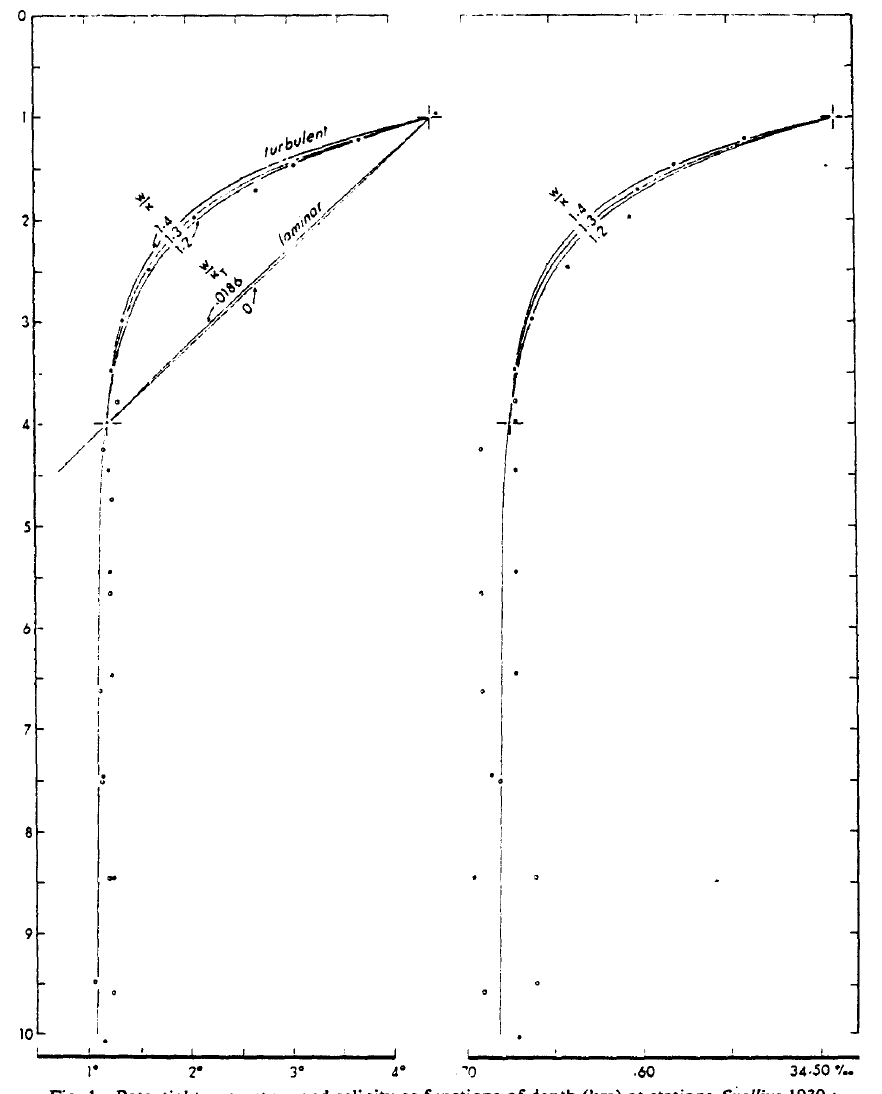
Fig. 21 Potential temperature and salinity as function of depth (km). Fig 1 of Walter Munks Abyssal Recipes (1966).

We know that a characteristic of turbulence is that it is dissipative. This means that turbulence requires an energy supply.

How much energy is required to maintain Munk’s predicted eddy diffusivity in the deep ocean?

If:

\[ E = \rho K_z N^2 A h , \]

where \(\rho = 1000\) kgm\(^3\) is a characteristic density, \(K_z = \)10\(^{-4}\) \(m^2s^{-1}\) is eddy diffusivity, \(N^2 = 10^{-5}\) s\(^{-2}\) is stratification, \(A = 3.6\) x \(10^14\) m\(^2\), is the surface area of the ocean below 1000 m and \(h = 4800 \) m, the thickness of the ocean below 1000 m.

\[ E \approx 1.7 \times 10^{12} \ \mathrm{W} = \mathbf{1.7} \ \mathrm{TW} \]

Where does this energy come from?

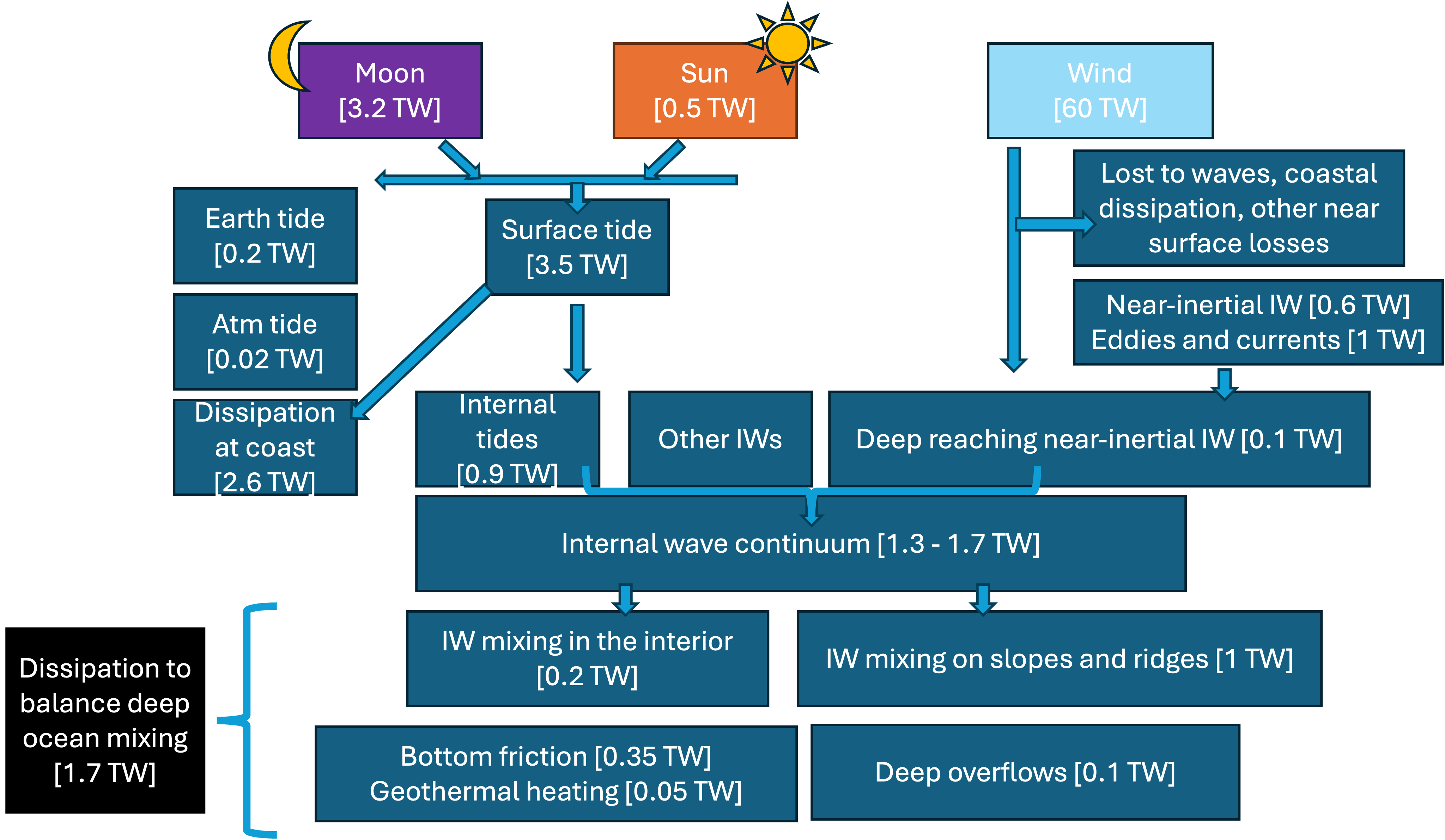
Fig. 22 Budget of energy flux to the deep ocean. Adapted and updated from [MW95].

You can see from this schematic that most of the energy is transferred to the deep ocean through internal waves. An overview of the state-of-art regarding internal waves is given by Mackinnon et al (2017) [MZW+17].